
Big O notation is a powerful tool used in computer science to describe the time complexity or space complexity of algorithms. It provides a standardized way to compare the efficiency of different algorithms in terms of their worst-case performance. Understanding Big O notation is essential for analyzing and designing efficient algorithms.
In this tutorial, we will cover the basics of Big O notation , its significance, and how to analyze the complexity of algorithms using Big O .

Table of Content
Big-O , commonly referred to as “ Order of ”, is a way to express the upper bound of an algorithm’s time complexity, since it analyses the worst-case situation of algorithm. It provides an upper limit on the time taken by an algorithm in terms of the size of the input. It’s denoted as O(f(n)) , where f(n) is a function that represents the number of operations (steps) that an algorithm performs to solve a problem of size n .
Big-O notation is used to describe the performance or complexity of an algorithm. Specifically, it describes the worst-case scenario in terms of time or space complexity.
Important Point:
Given two functions f(n) and g(n) , we say that f(n) is O(g(n)) if there exist constants c > 0 and n0 >= 0 such that f(n) for all n >= n0 .
In simpler terms, f(n) is O(g(n)) if f(n) grows no faster than c*g(n) for all n >= n 0 where c and n 0 are constants.

Big O notation is a mathematical notation used to describe the worst-case time complexity or efficiency of an algorithm or the worst-case space complexity of a data structure. It provides a way to compare the performance of different algorithms and data structures, and to predict how they will behave as the input size increases.
Big O notation is important for several reasons:
Below are some important Properties of Big O Notation:
For any function f(n), f(n) = O(f(n)).
Example:
If f(n) = O(g(n)) and g(n) = O(h(n)), then f(n) = O(h(n)).
Example:
f(n) = n 3 , g(n) = n 2 , h(n) = n 4 . Then f(n) = O(g(n)) and g(n) = O(h(n)). Therefore, f(n) = O(h(n)).
For any constant c > 0 and functions f(n) and g(n), if f(n) = O(g(n)), then cf(n) = O(g(n)).
Example:
f(n) = n, g(n) = n 2 . Then f(n) = O(g(n)). Therefore, 2f(n) = O(g(n)).
If f(n) = O(g(n)) and h(n) = O(g(n)), then f(n) + h(n) = O(g(n)).
Example:
f(n) = n 2 , g(n) = n 3 , h(n) = n 4 . Then f(n) = O(g(n)) and h(n) = O(g(n)). Therefore, f(n) + h(n) = O(g(n)).
If f(n) = O(g(n)) and h(n) = O(k(n)), then f(n) * h(n) = O(g(n) * k(n)).
Example:
f(n) = n, g(n) = n 2 , h(n) = n 3 , k(n) = n 4 . Then f(n) = O(g(n)) and h(n) = O(k(n)). Therefore, f(n) * h(n) = O(g(n) * k(n)) = O(n 5 ).
If f(n) = O(g(n)) and g(n) = O(h(n)), then f(g(n)) = O(h(n)).
Example:
f(n) = n 2 , g(n) = n, h(n) = n 3 . Then f(n) = O(g(n)) and g(n) = O(h(n)). Therefore, f(g(n)) = O(h(n)) = O(n 3 ).
Big-O notation is a way to measure the time and space complexity of an algorithm. It describes the upper bound of the complexity in the worst-case scenario. Let’s look into the different types of time complexities:
Linear time complexity means that the running time of an algorithm grows linearly with the size of the input.
Logarithmic time complexity means that the running time of an algorithm is proportional to the logarithm of the input size.
For example, a binary search algorithm has a logarithmic time complexity:
Quadratic time complexity means that the running time of an algorithm is proportional to the square of the input size.
For example, a simple bubble sort algorithm has a quadratic time complexity:
Cubic time complexity means that the running time of an algorithm is proportional to the cube of the input size.
For example, a naive matrix multiplication algorithm has a cubic time complexity:
Polynomial time complexity refers to the time complexity of an algorithm that can be expressed as a polynomial function of the input size n . In Big O notation, an algorithm is said to have polynomial time complexity if its time complexity is O(n k ) , where k is a constant and represents the degree of the polynomial.
Algorithms with polynomial time complexity are generally considered efficient, as the running time grows at a reasonable rate as the input size increases. Common examples of algorithms with polynomial time complexity include linear time complexity O(n) , quadratic time complexity O(n 2 ) , and cubic time complexity O(n 3 ) .
Exponential time complexity means that the running time of an algorithm doubles with each addition to the input data set.
For example, the problem of generating all subsets of a set is of exponential time complexity:
Factorial time complexity means that the running time of an algorithm grows factorially with the size of the input. This is often seen in algorithms that generate all permutations of a set of data.
Here’s an example of a factorial time complexity algorithm, which generates all permutations of an array:
If we plot the most common Big O notation examples, we would have graph like this:
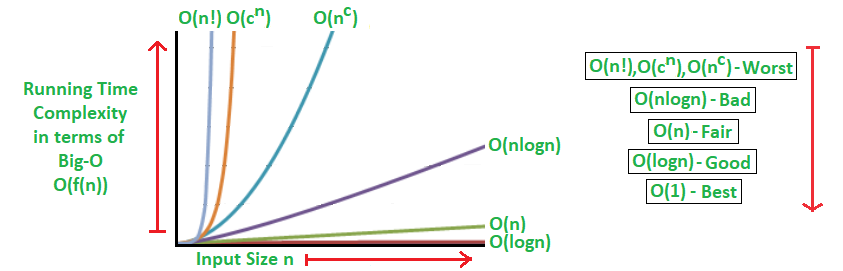
Big O notation is a mathematical notation used to describe the asymptotic behavior of a function as its input grows infinitely large. It provides a way to characterize the efficiency of algorithms and data structures.
1. Identify the Dominant Term:
2. Determine the Order of Growth:
3. Write the Big O Notation:
4. Simplify the Notation (Optional):
Example:
Below table illustrates the runtime analysis of different orders of algorithms as the input size (n) increases.
| n | log(n) | n | n * log(n) | n^2 | 2^n | n! |
|---|---|---|---|---|---|---|
| 10 | 1 | 10 | 10 | 100 | 1024 | 3628800 |
| 20 | 2.996 | 20 | 59.9 | 400 | 1048576 | 2.432902e+1818 |
Below table categorizes algorithms based on their runtime complexity and provides examples for each type.
| Type | Notation | Example Algorithms |
|---|---|---|
| Logarithmic | O(log n) | Binary Search |
| Linear | O(n) | Linear Search |
| Superlinear | O(n log n) | Heap Sort, Merge Sort |
| Polynomial | O(n^c) | Strassen’s Matrix Multiplication, Bubble Sort, Selection Sort, Insertion Sort, Bucket Sort |
| Exponential | O(c^n) | Tower of Hanoi |
| Factorial | O(n!) | Determinant Expansion by Minors, Brute force Search algorithm for Traveling Salesman Problem |
Below are the classes of algorithms and their execution times on a computer executing 1 million operation per second (1 sec = 10 6 μsec = 10 3 msec) :
Big O Notation Classes
Big O Analysis (number of operations) for n = 10